用JAVA实现的一种改进的K均值聚类算法流程
最近一直在搞这个改进算法,主要是涉及到特征降维和初始中心的选择。
通过分词的质量来实现降维在之前的博文中已经提到过了,用代码实现后,发现降维后的数据在时间上能提高很多,至于聚类的效果,因为自己也找不到很好的评定方案,所以也是个未知数,不过根据资料上的测试数据看来聚类的效果也是有提高的。
在降维过程中,我还将分词结果匹配了词性,比如只取名词和动词,对于一个语句的语义衡量也是需要去加深的地方。取指定词性的词后,文本特征的维度数是进一步的降低了,不过庖丁分词器分出来的词那叫一个多,这样省了也是省事不少,但是由于需要匹配词性,效率很降低不少,特别是在分词这一步,代码我在上篇文章贴出来了,这里很定还有更多的最优解,我的目的也就是实现了下功能。
下面来说一下聚类中心点的选择算法流程:
1.将文本空间向量特征标准化后作为聚类算法的输入,需要聚类的个数k、参数r和b。
2.根据空间向量通过公式得到非稀疏向量集合S1。
3.通过公式计算S1中的每个点的密度以及S1集合的平均密度
![]()
4. 得到S1中密度大于参数b*平均密度的点作为高密度集合S2
5. 初始中心集合M。
6.选择密度最大的点作为初始中心M的第一个点。
7.其他中心的选择:
1)分别得到中心点M中的每个点与集合S2中的点距离,选取最小值 。
2)从每个点的最小值中得到最大值作为新的初始中心加入中心集合M 。
8.剩下的就和标准K均值的算法差不多了。
对于距离的计算,欧几里得距离或者余弦夹角,这两种的结果差距也很大,欧几里得的聚类会相当的集中,迭代次数较多,我测试基本是在4次,而余弦夹角的结果会相对的分散而且迭代次数很少,一般在2次。
这个改进算法的资料来源于中山大学计算机科学系任江涛教授的一篇论文,文档中算法的描述不太详尽,自己数学也太烂了,没办法,琢磨了好久才把这个东西弄出来。
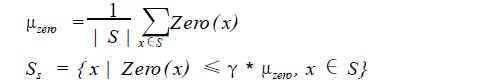
http://www.hidehai.com/html/y2010/564.html
你好,我的qq是490414333,可以把代码给我参考一下吗!谢谢啦!
你好,这个代码机器上已经不再了。 :sx: